Transformaciones tridimensionales

Las transformaciones de los objetos, son la Posición, la Rotación y la Escala.

Determinan la ubicación en el la escena mediante coordenadas trigonométricas en los ejes de coordenadas  x, y y z. Se refieren a todo el objeto.  La manera más fácil de conseguir las transformaciones básicas (traslación, rotación, escalación, en general las transformaciones afines) es utilizando matrices de transformación.

Coordenadas homogéneas

Nos será útil sustituir las coordenadas (x, y) por las coordenadas (xh, yh, h), llamadas coordenadas homogéneas.

Expresar posiciones en coordenadas homogéneas nos permite representar todas las ecuaciones de transformación geométrica como multiplicaciones de matriz. Se representan las coordenadas con vectores de columna de 3 elementos y las operaciones de transformación se expresan como matrices de 3 por 3.

Matrices de transformación en 3D más comunes

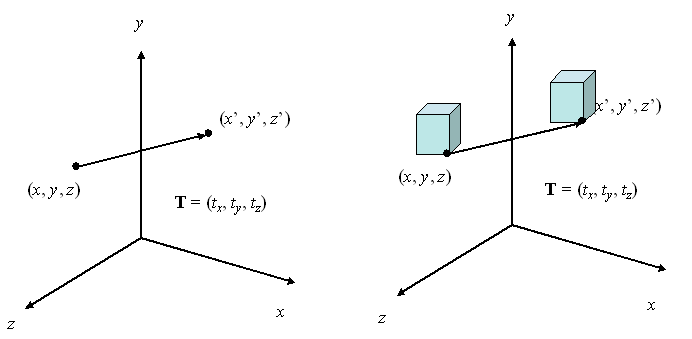
Traslación

En la representación homogénea tridimensional de las coordenadas, se traslada un punto de la posición P = (x, y, z) a la posición P’ = (x’, y’, z’) con la operación de matriz.

P’ = T x P

donde P y P’ son vectores columna como matrices, la matriz

Rotación

Para generar una transformación de rotación, debemos designar un eje de rotación respecto del cual girará el objeto, y la cantidad de rotación angular, es decir, un ángulo (θ).

Una rotación tridimensional se puede especificar alrededor de cualquier línea en el espacio.

Los ejes de rotación más fáciles de manejar son aquellos paralelos a los ejes de coordenadas.

Se forma una matriz de rotación inversa al sustituir el ángulo de rotación θ por –θ. Los valores negativos para los ángulos de rotación generan rotaciones en una dirección en el sentido del reloj, de modo que se produce la matriz identidad cuando se multiplica cualquier matriz de rotación por su inverso

Escalación

La matriz para la transformación de escalación de una posición P = (x, y, z) con respecto del origen de las coordenadas se puede escribir como:

Donde ex, ey, y ez pueden tener cualquier valor positivo (valores de escalación en cada uno de los ejes, si estos no son iguales, se cambian las dimensiones relativas en el objeto).

La escalación con respecto a una posición fija seleccionada se puede obtener con la siguiente secuencia de transformación:

1. Se traslada el punto fijo al origen.

2. Se escala el objeto con respecto al origen.

3. Se traslada el punto fijo a su posición original.

Conclusión

Cabe mencionar que todos los gráficos por computadora que han existido, hay requerido de algún modelo matemático o cálculos vitales para su construcción. Y no es la excepción en la actualidad, pues con las transformaciones tridimensionales se utilizan matrices de transformación donde se expresan y se resuelven posiciones se utilizan cálculos.

Bibliografía

http://arquimedes.matem.unam.mx/pasados/CursoDescartes_3.853/Graficas3D.html
http://mimosa.pntic.mec.es/clobo/geoweb/espa2.htm